שלום,
נראה שכבר הכרתם את אאוריקה. בטח כבר גיליתם כאן דברים מדהימים, אולי כבר שאלתם שאלות וקיבלתם תשובות טובות.
נשמח לראות משהו מכם בספר האורחים שלנו: איזו מילה טובה, חוות דעת, עצה חכמה לשיפור או כל מה שיש לכם לספר לנו על אאוריקה, כפי שאתם חווים אותה.
»
«
 מהי סימטריה?
מהי סימטריה?
הסימטריה (Symmetric) הפשוטה שאנו מכירים היא שיקוף של צד אחד בצד השני, משני צידי קו דמיוני העובר ביניהם.
הסימטריה מופיעה בטבע כצורה של סדר, בתוך מגוון של צורות לא מסודרות, האדם שהוקף במגוון אדיר של צורות מסביבו, זיהה כבר מימי קדם את הסדר והיופי שבסימטריה והשתמש בהם באמנות ובבניה. הסימטריה היא גם אחד הדברים שמקשרים בין אמנות למדע.
מסתבר שאנו מתוכנתים ביולוגית לראות בסימטריה יופי. גם אם זה אינו המרכיב היחידי של היופי, אנשים עם מבנה פנים סימטרי נתפסים על ידינו בתור יפים יותר.
ניתן לראות סימטריה בטבע ובעצמים שונים בחיי היום יום. כנפי הפרפר ועלי הפרח הם דוגמאות טבעיות לסימטריה. אפילו בנופים המשתקפים במים ניתן לראות סימטריה מרהיבה.
בגאומטריה יש שני סוגים של סימטריה - סימטריה שיקופית וסיבובית. "סימטריה שיקופית" היא סימטריה שבה יש מעין השתקפות של צד אחד בצד השני. קו השיקוף נקרא קו סימטריה. זהו קו דמיוני שחותך את העצם לשניים. שני הצדדים שבצידי קו זה דומים. יש גם צורות שיש להן "סימטריה סיבובית". היא קיימת כשקיים סיבוב כלשהו (אך לא סיבוב שלם) שבו הצורה מועתקת בדייקנות.
#פעילות קטנה:
נסו למצוא ולצלם 5 חפצים סימטריים שיש בביתכם או בכיתה.
הנה הסבר על הסימטריה וסימטריות מסוגים שונים בטבע (מתורגם):
http://youtu.be/3drtbPZF9yc
על הסימטריה וקו הסימטריה:
http://youtu.be/6qNB2LsgC8Y
סרטון אמנותי שמציג סימטריה בנושאים וההתייחסות של מרכיבים שאנו רואים בו:
http://youtu.be/zEQskIsHKT8
קטעים מסרטיו של במאי הקולנוע ווס אנדרסון שסגנונו הסימטרי הפך לסימן ההיכר שלו:
https://youtu.be/fq4sN2vqKq4
בואו נבדוק את הסימטריה בתמונות שונות:
http://youtu.be/_TdOD2f_KEk
יש מי שהחליטו בעולם התעופה לשבור את הסימטריה (עברית):
https://youtu.be/djRAfVSgLWY
והרצאה ארוכה ומעניינת באנגלית על הסימטריה במדע הגאומטריה ועל המתמטיקאי אווריסט גלואה שעסק בה (מתורגם):
http://youtu.be/415VX3QX4cU?long=yes
 איפה בטבע אפשר לראות משושים?
איפה בטבע אפשר לראות משושים?
המשושה הוא צורה משוכללת מהמעטות שבהן ניתן לרצף מישור בצורה מחזורית, מבלי להשאיר חורים. אמנם גם הריבוע והמשולש מאפשרים זאת, אבל משלושתם המשושה הוא הצורה הקרובה ביותר לעיגול.
יש מקרים רבים בטבע שבהם ניתן לראות משושים. כך למשל חומרים שונים בטבע שנוטים להפוך למוצקים בצורה של משושים. רואים זאת לא מעט בצורות של לבה שהפכה לאבן בזלת מוצקה ונסדקה בצורת משושים. אתרים כמו בריכת המשושים שברמת הגולן, מערת פינגל בסקוטלנד או סוללת הענק באירלנד מדגימים זאת היטב (ראו אותם באאוריקה בתגית "משושי בזלת"). ניתן לראות התייבשות בצורת משושים גם באגמי מלח ובימות מלח שבהם נותר המשקע של מלח הבישול בצורת משושים.
גם התאים שבכוורת הדבורים בנויים כמשושים. הם עשויים משעווה שאותה מייצרת כל דבורה בעצמה. נדרש דבש רב כדי לבנות את התאים הללו בצורה חזקה וטובה, כך שהדבש לא יגלוש החוצה והדבורים יוכלו להיכנס לתוכם. המשושה היא הצורה הכי חסכונית מבחינת כמות השעווה הנדרשת לבניה, שעדיין מייצרת את מקום האיחסון הרב ביותר בכל תא ותא. לכן צורת המשושים היא היעילה ביותר מבחינה אדריכלית ומבחינה מתמטית.
הנה סרטון שמציג את היעילות שבבנייה במשושים (מתורגם):
http://youtu.be/QEzlsjAqADA?t=6s
על פתיתי שלג, שבהם המשושים הם הנפוצים ביותר:
http://youtu.be/rbW6MsXfPYU
ומשושה מושלם שהתגלה על הקוטב הצפוני של כוכב הלכת סאטורן:
http://youtu.be/qzL194jiTyY
 מהי רקורסיה?
מהי רקורסיה?
רקורסיה היא הליך שפונה לעצמו. קצת יותר מורכב הוא ההסבר או המיקוד של בעיה כללית אל בעיה "קטנה" יותר, אך זהה לבעיה המקורית.
לפיכך, גם הגדרה רקורסיבית היא הגדרה שחייבת לפנות לאותה הגדרה, אבל בתנאים שונים. ותמיד יהיה שם תנאי עצירה, כדי שהרקורסיה לא תהיה אינסופית..
הגדרה אחרת לרקורסיה היא "הגדרת בעיה במונחים של עצמה".
רוצים דוגמה:
"אם הבנת מהי רקורסיה, חזור אל הדף ממנו הגעת. אם לא – קרא בדף זה מהי רקורסיה".
הדוגמה הזו מסבירה בדיוק את הרקורסיה, כי תנאי העצירה הוא "אם הבנת.." ,בעוד ש"אם לא" אז חוזרים לאותה דוגמה כדי ללמוד מהי רקורסיה מחדש ולבסוף מבינים שהרקורסיה היא מה שאתה מתבקש לעשות...
#בתכנות
מתכנתים משתמשים הרבה ברקורסיה. הם מתארים פונקציה רקורסיבית כ"פונקציה שקוראת לעצמה". נכון היה יותר לומר שפונקציה כזו קוראת לעותק של עצמה אבל בכל מקרה הפונקציה הזו קוראת לעצמה בלולאה (Loop) עד שלא ניתן יותר לעשות זאת - כלומר, יש תנאי יציאה שמבטיח שהיא לא תעשה את זה עד אינסוף ויהיה stack overflow...
לרוב נותנים לרקורסיה כזו את הדוגמה של חישוב n-עצרת במתמטיקה (=מכפלת 1 כפול 2 כפול 3… עד כפול n).
ואגב, הנה משפט נכון ומשעשע, אחד הממים השנונים של האינטרנט הגיקי: "כדי להגדיר רקורסיה, קודם-כל צריך להגדיר רקורסיה.."
הנה הסבר יפה לרקורסיה עם דוגמה קולנועית:
https://youtu.be/Q83nN97LVOU
סרטון שמדגים איך רקורסיה עובדת כשעושים בעזרתה גרפיקה ממוחשבת:
http://youtu.be/ghZKKaZkzrE
כניסה פנימה לפרקטל - צורה גרפית שנקראת "משולש סירפינסקי" ונבנתה בפונקציה רקורסיבית:
http://youtu.be/P5EkdJRtF-4
בקצרה:
https://youtu.be/rf60MejMz3E
והסבר למתכנתים (עברית):
https://youtu.be/B19qH3XFnxY?long=yes
 מהן מנדלות? מהי מנדלה?
מהן מנדלות? מהי מנדלה?
מַנְדָּלָה היא ציור מעגל שנובע ממרכזו. המנדלה מורכבת מעיגול שבו מוצג ציור, או סימן גרפי דומה. אמונות שונות ותרבויות שונות, במיוחד הבודהיזם וההינדואיזם, קידשו את המנדלה וראו בה סמל מרכזי.
בדתות של הודו ראו בה סמל ליקום ולצורה שלו.
יש למנדלה שימוש חשוב בטיפולים באמנות, בעבודה טיפולית והיא משמשת ככלי להתפתחות רוחנית בהינדואיזם ובבודהיזם.
מקור המילה מנדלה הוא משפת הסנסקריט ההודית, שבה פירושה הוא "מרכז", או "מעגל", רמז למעגל המקודש של ההודים.
הנה הסבר על המנדלה (עברית):
http://youtu.be/dezE3_aCGHQ?t=42s
על המנדלה באנגלית:
https://youtu.be/gYBBsxrsJOw
הכהן הגדול של המנדלות בישראל, מסביר על המנדלה (עברית):
http://youtu.be/eZWKJf4JxDE
ומדריך ראשוני לציור מנדלות (עברית):
http://youtu.be/cCyBqOBCSeE
 מהם מגדלי האנוי?
מהם מגדלי האנוי?
מגדלי האנוי הם שם של חידה מפורסמת שהומצאה על ידי המתמטיקאי הצרפתי אדוארד לוקאס בשנת 1883. ב"מגדלי הנוי" נתון מגדל עם דיסקיות שהיקפן הולך ונעשה קטן ככל שהן עליונות (הרחבות למטה). מטרת החידה היא להעביר את כל המגדל בשלמותו לאחד משני העמודים הריקים שלידו. כמובן שיש להעביר את הדיסקיות במה שפחות צעדים וכמה שיותר מהר.
החידה משמשת ללימוד מתמטיקה ומדעי המחשב ולהמחשת מושגים כמו רקורסיה (ראו באאוריקה בתגית "רקורסיה"). עוד פרט מעניין - אם נסמן בנקודה כל מצב חוקי במשחק מגדלי האנוי, ונקשר בקווים את המצבים שבהם אפשר לעבור מאחד לשני, נקבל למול עינינו את גרף המשחק, בצורה של הפרקטל המוכר כ"משולש שרפינסקי".
אגב, לוקאס המציא גם אגדה שמדובר במקדש בראהמי שבו הכהנים מעבירים מגדל בן 64 דיסקיות. על פי האגדה שלו, כשיסיימו הכהנים את עבודתם, יגיע גם סוף העולם..
ישנם כללים להעברה:
א. בכל שלב תעבור רק דיסקית אחת מקום.
ב. אסור שיהיה מצב שדיסקית תהיה מונחת על דיסקית קטנה יותר.
הנה דרך לפתרון של חידת מגדלי האנוי:
http://youtu.be/BMkOBNZHcIs
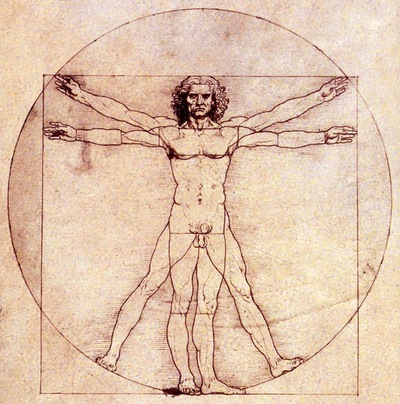 מהו האדם הוויטרובי של לאונרדו דה וינצ'י?
מהו האדם הוויטרובי של לאונרדו דה וינצ'י?
האדם הוויטרובי הוא אולי הרישום המפורסם ביותר של האמן לאונרדו דה וינצ'י. הרישום, שנקרא גם "קאנון היחסים", צוייר בשנת 1490 ומתאר דרך הפרופורציות והסימטריה של הגוף האנושי את השלמות וההרמוניה שראו מדעני ואמני התקופה. בראש אותם המגלים עמד לאונרדו עצמו - אולי החוקר, היוצר, המהנדס והממציא החשוב בתולדות האנושות.
הרישום הזה של לאונרדו נחשב מיצירות האמנות המוכרות ואף החשובות של הרנסאנס האיטלקי. מהות התקופה הייתה הגילוי מחדש של חוקים אמנותיים, אסתטיים ומדעיים, שהיו ידועים בתרבויות העבר הרומיות, היווניות ואלה שלפניהן.
חלק מהפלאים שהתגלו שוב ברנסאנס היו קשורים ביחסים המתמטיים המדוייקים שבטבע. לאונרדו רשם את "האדם הוויטרובי" לאחר שעיין בפרופורציות גוף האדם שצויינו בספרו של האדריכל הרומאי ויטרוביוס "על אודות האדריכלות".
הנה הסבר מתורגם על האדם הוויטרובי של לאונרדו דה וינצ'י (מתורגם):
http://youtu.be/aMsaFP3kgqQ?t=14s
בשנות ה-80 השתמשה האוניברסיטה הפתוחה באדם הוויטרובי כפתיח לשידורי הטלוויזיה שלה:
https://youtu.be/I1ZVjfUaz9M
ניסיון "לשדרג" את האדם הוויטרובי למאה ה-21:
http://youtu.be/jwnTvv7NaJA
וסרט תיעודי על האדם הויטרובי:
https://youtu.be/GGUOtwDhyzc?long=yes
 מהם פתיתי השלג ואיך הם נוצרים?
מהם פתיתי השלג ואיך הם נוצרים?
פתיתי שלג הם פתיתי קרח גדולים וגבישיים שנופלים מהעננים אל הקרקע. פתיתי השלג הם קלים בזכות האוויר שיש בהם. פתיתי שלג עשויים מגבישי שלג קטנטנים שנצמדים זה לזה.
הצורות המופלאות של פתיתי השלג עשויות במגוון אדיר וניתן לומר שאין שני פתיתי שלג זהים זה לזה. רבות מצורות פתיתי השלג הם פרקטליות, צורות שבהן ככל שמעמיקים ומתקרבים, רואים עוד ועוד מאותן צורות.
הדוגמאות הנפוצות ביותר בפתיתי השלג הן בצורת המשושה. זו שוב הצורה של המשושים, שכל כך נפוצה בטבע (ראו באאוריקה בתגית "משושים").
חלקים גדולים מכדור הארץ מכוסים בשלג. יש אזורים שבהם השלג מכסה את האדמה רק בעונת החורף ולקראת הקיץ השלגים מפשירים. באזורים אחרים, כמו הקוטב הצפוני והקוטב הדרומי ופסגות ההרים הגבוהים, האדמה מושלגת בכל עונות השנה.
כך נוצר השלג ואיך לכל אחד מפתיתי השלג יש צורה משלו (עברית):
https://youtu.be/omDSofC8L0E?end=1m17s
ההסבר לפתיתי השלג הללו (מתורגם):
https://youtu.be/FwGH4gulLX4
הצורות המופלאות של פתיתי השלג שיורדים בחורף:
http://youtu.be/s1lBbmQmpk0
קפיאת פתיתי השלג והתגבשות תחת מיקרוסקופ:
https://youtu.be/q-PQk2-Po-g
על תוכנה שפותחה כדי לדמות את פתיתי השלג הללו באופן מדעי (מתורגם):
http://youtu.be/UtHsFVmHdZY
והפשרת השלגים בתחילת הקיץ:
http://youtu.be/MwdWMmFeXIo
 מהו משולש סירפינסקי?
מהו משולש סירפינסקי?
משולש שרפינסקי, שנקרא גם ספוג שרפינסקי או משולש סירפינסקי, הוא אחד הפרקטלים המפורסמים. את ההיכרות עימו עשו המתמטיקאים בשנת 1915. המשולש קיבל את שמו מהמתמטיקאי הפולני שתיאר אותו לראשונה, ואצלב שרפינסקי.
משולש שרפינסקי הוא דוגמה מצוינת ופשוטה במיוחד לפרקטל, צורה שמורכבת מעותקים מוקטנים של עצמה, עד אינסוף. הוא בנוי משלושה עותקים שלו שהוקטנו בחצי שוב ושוב.
הנה משולש סרפינסקי שלא נגמר, להדגמת הרקורסיה הפשוטה:
http://youtu.be/QsMvoui5WlQ?t=10s
סרט אפל מתורגם ומדהים על הפרקטלים ומשולש שרפינסקי בתוכם (מתורגם):
https://youtu.be/0C75vRVL5lE
סרטון בגרפיקת מחשב של "משולש סירפינסקי" שנבנה ברקורסיה בתלת-מימד:
http://youtu.be/P5EkdJRtF-4
משולש שרפינסקי מסוכריות של החג הנוצרי המעט מפחיד "ליל כל הקדושים":
http://youtu.be/z8ZWlUamNPI
וכך יוצרים פרקטלים כמו משולש סרפינסקי:
http://youtu.be/XwWyTts06tU?t=1m22s
 מהו פאי?
מהו פאי?
הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes

הסימטריה (Symmetric) הפשוטה שאנו מכירים היא שיקוף של צד אחד בצד השני, משני צידי קו דמיוני העובר ביניהם.
הסימטריה מופיעה בטבע כצורה של סדר, בתוך מגוון של צורות לא מסודרות, האדם שהוקף במגוון אדיר של צורות מסביבו, זיהה כבר מימי קדם את הסדר והיופי שבסימטריה והשתמש בהם באמנות ובבניה. הסימטריה היא גם אחד הדברים שמקשרים בין אמנות למדע.
מסתבר שאנו מתוכנתים ביולוגית לראות בסימטריה יופי. גם אם זה אינו המרכיב היחידי של היופי, אנשים עם מבנה פנים סימטרי נתפסים על ידינו בתור יפים יותר.
ניתן לראות סימטריה בטבע ובעצמים שונים בחיי היום יום. כנפי הפרפר ועלי הפרח הם דוגמאות טבעיות לסימטריה. אפילו בנופים המשתקפים במים ניתן לראות סימטריה מרהיבה.
בגאומטריה יש שני סוגים של סימטריה - סימטריה שיקופית וסיבובית. "סימטריה שיקופית" היא סימטריה שבה יש מעין השתקפות של צד אחד בצד השני. קו השיקוף נקרא קו סימטריה. זהו קו דמיוני שחותך את העצם לשניים. שני הצדדים שבצידי קו זה דומים. יש גם צורות שיש להן "סימטריה סיבובית". היא קיימת כשקיים סיבוב כלשהו (אך לא סיבוב שלם) שבו הצורה מועתקת בדייקנות.
#פעילות קטנה:
נסו למצוא ולצלם 5 חפצים סימטריים שיש בביתכם או בכיתה.
הנה הסבר על הסימטריה וסימטריות מסוגים שונים בטבע (מתורגם):
http://youtu.be/3drtbPZF9yc
על הסימטריה וקו הסימטריה:
http://youtu.be/6qNB2LsgC8Y
סרטון אמנותי שמציג סימטריה בנושאים וההתייחסות של מרכיבים שאנו רואים בו:
http://youtu.be/zEQskIsHKT8
קטעים מסרטיו של במאי הקולנוע ווס אנדרסון שסגנונו הסימטרי הפך לסימן ההיכר שלו:
https://youtu.be/fq4sN2vqKq4
בואו נבדוק את הסימטריה בתמונות שונות:
http://youtu.be/_TdOD2f_KEk
יש מי שהחליטו בעולם התעופה לשבור את הסימטריה (עברית):
https://youtu.be/djRAfVSgLWY
והרצאה ארוכה ומעניינת באנגלית על הסימטריה במדע הגאומטריה ועל המתמטיקאי אווריסט גלואה שעסק בה (מתורגם):
http://youtu.be/415VX3QX4cU?long=yes

המשושה הוא צורה משוכללת מהמעטות שבהן ניתן לרצף מישור בצורה מחזורית, מבלי להשאיר חורים. אמנם גם הריבוע והמשולש מאפשרים זאת, אבל משלושתם המשושה הוא הצורה הקרובה ביותר לעיגול.
יש מקרים רבים בטבע שבהם ניתן לראות משושים. כך למשל חומרים שונים בטבע שנוטים להפוך למוצקים בצורה של משושים. רואים זאת לא מעט בצורות של לבה שהפכה לאבן בזלת מוצקה ונסדקה בצורת משושים. אתרים כמו בריכת המשושים שברמת הגולן, מערת פינגל בסקוטלנד או סוללת הענק באירלנד מדגימים זאת היטב (ראו אותם באאוריקה בתגית "משושי בזלת"). ניתן לראות התייבשות בצורת משושים גם באגמי מלח ובימות מלח שבהם נותר המשקע של מלח הבישול בצורת משושים.
גם התאים שבכוורת הדבורים בנויים כמשושים. הם עשויים משעווה שאותה מייצרת כל דבורה בעצמה. נדרש דבש רב כדי לבנות את התאים הללו בצורה חזקה וטובה, כך שהדבש לא יגלוש החוצה והדבורים יוכלו להיכנס לתוכם. המשושה היא הצורה הכי חסכונית מבחינת כמות השעווה הנדרשת לבניה, שעדיין מייצרת את מקום האיחסון הרב ביותר בכל תא ותא. לכן צורת המשושים היא היעילה ביותר מבחינה אדריכלית ומבחינה מתמטית.
הנה סרטון שמציג את היעילות שבבנייה במשושים (מתורגם):
http://youtu.be/QEzlsjAqADA?t=6s
על פתיתי שלג, שבהם המשושים הם הנפוצים ביותר:
http://youtu.be/rbW6MsXfPYU
ומשושה מושלם שהתגלה על הקוטב הצפוני של כוכב הלכת סאטורן:
http://youtu.be/qzL194jiTyY

רקורסיה היא הליך שפונה לעצמו. קצת יותר מורכב הוא ההסבר או המיקוד של בעיה כללית אל בעיה "קטנה" יותר, אך זהה לבעיה המקורית.
לפיכך, גם הגדרה רקורסיבית היא הגדרה שחייבת לפנות לאותה הגדרה, אבל בתנאים שונים. ותמיד יהיה שם תנאי עצירה, כדי שהרקורסיה לא תהיה אינסופית..
הגדרה אחרת לרקורסיה היא "הגדרת בעיה במונחים של עצמה".
רוצים דוגמה:
"אם הבנת מהי רקורסיה, חזור אל הדף ממנו הגעת. אם לא – קרא בדף זה מהי רקורסיה".
הדוגמה הזו מסבירה בדיוק את הרקורסיה, כי תנאי העצירה הוא "אם הבנת.." ,בעוד ש"אם לא" אז חוזרים לאותה דוגמה כדי ללמוד מהי רקורסיה מחדש ולבסוף מבינים שהרקורסיה היא מה שאתה מתבקש לעשות...
#בתכנות
מתכנתים משתמשים הרבה ברקורסיה. הם מתארים פונקציה רקורסיבית כ"פונקציה שקוראת לעצמה". נכון היה יותר לומר שפונקציה כזו קוראת לעותק של עצמה אבל בכל מקרה הפונקציה הזו קוראת לעצמה בלולאה (Loop) עד שלא ניתן יותר לעשות זאת - כלומר, יש תנאי יציאה שמבטיח שהיא לא תעשה את זה עד אינסוף ויהיה stack overflow...
לרוב נותנים לרקורסיה כזו את הדוגמה של חישוב n-עצרת במתמטיקה (=מכפלת 1 כפול 2 כפול 3… עד כפול n).
ואגב, הנה משפט נכון ומשעשע, אחד הממים השנונים של האינטרנט הגיקי: "כדי להגדיר רקורסיה, קודם-כל צריך להגדיר רקורסיה.."
הנה הסבר יפה לרקורסיה עם דוגמה קולנועית:
https://youtu.be/Q83nN97LVOU
סרטון שמדגים איך רקורסיה עובדת כשעושים בעזרתה גרפיקה ממוחשבת:
http://youtu.be/ghZKKaZkzrE
כניסה פנימה לפרקטל - צורה גרפית שנקראת "משולש סירפינסקי" ונבנתה בפונקציה רקורסיבית:
http://youtu.be/P5EkdJRtF-4
בקצרה:
https://youtu.be/rf60MejMz3E
והסבר למתכנתים (עברית):
https://youtu.be/B19qH3XFnxY?long=yes

מַנְדָּלָה היא ציור מעגל שנובע ממרכזו. המנדלה מורכבת מעיגול שבו מוצג ציור, או סימן גרפי דומה. אמונות שונות ותרבויות שונות, במיוחד הבודהיזם וההינדואיזם, קידשו את המנדלה וראו בה סמל מרכזי.
בדתות של הודו ראו בה סמל ליקום ולצורה שלו.
יש למנדלה שימוש חשוב בטיפולים באמנות, בעבודה טיפולית והיא משמשת ככלי להתפתחות רוחנית בהינדואיזם ובבודהיזם.
מקור המילה מנדלה הוא משפת הסנסקריט ההודית, שבה פירושה הוא "מרכז", או "מעגל", רמז למעגל המקודש של ההודים.
הנה הסבר על המנדלה (עברית):
http://youtu.be/dezE3_aCGHQ?t=42s
על המנדלה באנגלית:
https://youtu.be/gYBBsxrsJOw
הכהן הגדול של המנדלות בישראל, מסביר על המנדלה (עברית):
http://youtu.be/eZWKJf4JxDE
ומדריך ראשוני לציור מנדלות (עברית):
http://youtu.be/cCyBqOBCSeE
צורות טבעיות

מגדלי האנוי הם שם של חידה מפורסמת שהומצאה על ידי המתמטיקאי הצרפתי אדוארד לוקאס בשנת 1883. ב"מגדלי הנוי" נתון מגדל עם דיסקיות שהיקפן הולך ונעשה קטן ככל שהן עליונות (הרחבות למטה). מטרת החידה היא להעביר את כל המגדל בשלמותו לאחד משני העמודים הריקים שלידו. כמובן שיש להעביר את הדיסקיות במה שפחות צעדים וכמה שיותר מהר.
החידה משמשת ללימוד מתמטיקה ומדעי המחשב ולהמחשת מושגים כמו רקורסיה (ראו באאוריקה בתגית "רקורסיה"). עוד פרט מעניין - אם נסמן בנקודה כל מצב חוקי במשחק מגדלי האנוי, ונקשר בקווים את המצבים שבהם אפשר לעבור מאחד לשני, נקבל למול עינינו את גרף המשחק, בצורה של הפרקטל המוכר כ"משולש שרפינסקי".
אגב, לוקאס המציא גם אגדה שמדובר במקדש בראהמי שבו הכהנים מעבירים מגדל בן 64 דיסקיות. על פי האגדה שלו, כשיסיימו הכהנים את עבודתם, יגיע גם סוף העולם..
ישנם כללים להעברה:
א. בכל שלב תעבור רק דיסקית אחת מקום.
ב. אסור שיהיה מצב שדיסקית תהיה מונחת על דיסקית קטנה יותר.
הנה דרך לפתרון של חידת מגדלי האנוי:
http://youtu.be/BMkOBNZHcIs

האדם הוויטרובי הוא אולי הרישום המפורסם ביותר של האמן לאונרדו דה וינצ'י. הרישום, שנקרא גם "קאנון היחסים", צוייר בשנת 1490 ומתאר דרך הפרופורציות והסימטריה של הגוף האנושי את השלמות וההרמוניה שראו מדעני ואמני התקופה. בראש אותם המגלים עמד לאונרדו עצמו - אולי החוקר, היוצר, המהנדס והממציא החשוב בתולדות האנושות.
הרישום הזה של לאונרדו נחשב מיצירות האמנות המוכרות ואף החשובות של הרנסאנס האיטלקי. מהות התקופה הייתה הגילוי מחדש של חוקים אמנותיים, אסתטיים ומדעיים, שהיו ידועים בתרבויות העבר הרומיות, היווניות ואלה שלפניהן.
חלק מהפלאים שהתגלו שוב ברנסאנס היו קשורים ביחסים המתמטיים המדוייקים שבטבע. לאונרדו רשם את "האדם הוויטרובי" לאחר שעיין בפרופורציות גוף האדם שצויינו בספרו של האדריכל הרומאי ויטרוביוס "על אודות האדריכלות".
הנה הסבר מתורגם על האדם הוויטרובי של לאונרדו דה וינצ'י (מתורגם):
http://youtu.be/aMsaFP3kgqQ?t=14s
בשנות ה-80 השתמשה האוניברסיטה הפתוחה באדם הוויטרובי כפתיח לשידורי הטלוויזיה שלה:
https://youtu.be/I1ZVjfUaz9M
ניסיון "לשדרג" את האדם הוויטרובי למאה ה-21:
http://youtu.be/jwnTvv7NaJA
וסרט תיעודי על האדם הויטרובי:
https://youtu.be/GGUOtwDhyzc?long=yes

פתיתי שלג הם פתיתי קרח גדולים וגבישיים שנופלים מהעננים אל הקרקע. פתיתי השלג הם קלים בזכות האוויר שיש בהם. פתיתי שלג עשויים מגבישי שלג קטנטנים שנצמדים זה לזה.
הצורות המופלאות של פתיתי השלג עשויות במגוון אדיר וניתן לומר שאין שני פתיתי שלג זהים זה לזה. רבות מצורות פתיתי השלג הם פרקטליות, צורות שבהן ככל שמעמיקים ומתקרבים, רואים עוד ועוד מאותן צורות.
הדוגמאות הנפוצות ביותר בפתיתי השלג הן בצורת המשושה. זו שוב הצורה של המשושים, שכל כך נפוצה בטבע (ראו באאוריקה בתגית "משושים").
חלקים גדולים מכדור הארץ מכוסים בשלג. יש אזורים שבהם השלג מכסה את האדמה רק בעונת החורף ולקראת הקיץ השלגים מפשירים. באזורים אחרים, כמו הקוטב הצפוני והקוטב הדרומי ופסגות ההרים הגבוהים, האדמה מושלגת בכל עונות השנה.
כך נוצר השלג ואיך לכל אחד מפתיתי השלג יש צורה משלו (עברית):
https://youtu.be/omDSofC8L0E?end=1m17s
ההסבר לפתיתי השלג הללו (מתורגם):
https://youtu.be/FwGH4gulLX4
הצורות המופלאות של פתיתי השלג שיורדים בחורף:
http://youtu.be/s1lBbmQmpk0
קפיאת פתיתי השלג והתגבשות תחת מיקרוסקופ:
https://youtu.be/q-PQk2-Po-g
על תוכנה שפותחה כדי לדמות את פתיתי השלג הללו באופן מדעי (מתורגם):
http://youtu.be/UtHsFVmHdZY
והפשרת השלגים בתחילת הקיץ:
http://youtu.be/MwdWMmFeXIo

משולש שרפינסקי, שנקרא גם ספוג שרפינסקי או משולש סירפינסקי, הוא אחד הפרקטלים המפורסמים. את ההיכרות עימו עשו המתמטיקאים בשנת 1915. המשולש קיבל את שמו מהמתמטיקאי הפולני שתיאר אותו לראשונה, ואצלב שרפינסקי.
משולש שרפינסקי הוא דוגמה מצוינת ופשוטה במיוחד לפרקטל, צורה שמורכבת מעותקים מוקטנים של עצמה, עד אינסוף. הוא בנוי משלושה עותקים שלו שהוקטנו בחצי שוב ושוב.
הנה משולש סרפינסקי שלא נגמר, להדגמת הרקורסיה הפשוטה:
http://youtu.be/QsMvoui5WlQ?t=10s
סרט אפל מתורגם ומדהים על הפרקטלים ומשולש שרפינסקי בתוכם (מתורגם):
https://youtu.be/0C75vRVL5lE
סרטון בגרפיקת מחשב של "משולש סירפינסקי" שנבנה ברקורסיה בתלת-מימד:
http://youtu.be/P5EkdJRtF-4
משולש שרפינסקי מסוכריות של החג הנוצרי המעט מפחיד "ליל כל הקדושים":
http://youtu.be/z8ZWlUamNPI
וכך יוצרים פרקטלים כמו משולש סרפינסקי:
http://youtu.be/XwWyTts06tU?t=1m22s

הפאי הוא מספר אי רציונאלי, מציין את היחס בין היקף מעגל לקוטרו. זהו מספר מסתורי, שמתמטיקאים וחובבי מתמטיקה מוקסמים ממנו כבר דורות רבים. ערכו של פאי שווה בקירוב ל 3.14.
הפאי מסומן באות היוונית π. הבבלים, ממציאי הגלגל, גילו אותו כבר לפני ששת אלפים שנה. התגלית של התופעה המרתקת של פאי, הייתה שבכל גודל מעגל שהוא, תוצאת החילוק של היקף המעגל ברדיוס שלו תהיה תמיד אותו המספר. 4000 שנה אחריהם, הצליחו מדעני מצרים העתיקה להגיע לערך מקורב של פאי. ארכימדס היווני הציג לראשונה, כבר במאה ה-3 לפני הספירה, שיטה שמאפשרת לאמוד את π.
הראשון שהצליח לחשב את פיי בדיוק גבוה היה אויילר. פיתוח החשבון הדיפרנציאלי והאינטגרלי סייע לו מאד והוא חישב את פאי עד 153 ספרות אחרי הנקודה. כמו הרבה דברים שאויילר תרם למתמטיקה, הוא גם זה שהעניק לפיי את שמו.
כיום, בעידן המחשב, המתמטיקאים עובדים על אלגוריתמים ונוסחאות אלגנטיות לחישוב פאי. השיא שנקבע עד 2011 הוא של 10 טריליון ספרות אחרי הנקודה!
הנה סרטון על משמעותו של הפיי (מתורגם):
http://youtu.be/9a5vHXsUvUw?t=13s
שיר לימודי באנגלית, להיכרות עם חישוב פאי:
http://youtu.be/eiHWHT_8WrE
מלחין שהחליט להלחין את המספר וכך לזכור אותו:
https://youtu.be/wM-x3pUcdeo
והביטוי המוסיקלי של המספר פאי ויחס הזהב שבנוי עליו:
https://youtu.be/9mozmHgg9Sk?long=yes
מהו ארכיטיפ? מהם ארכיטיפים?
ארכיטיפים (Archetypes) הם תבניות סימליות משותפות לעולם כולו. הארכיטיפים נמצאים בכל העולם ובכל התרבויות האנושיות כולן. הארכיטיפים הם תבניות של תפקידים שונים בחיים.
בין הארכיטיפים הידועים ניתן למצוא את הגיבור, האנדרדוג, הלוחם, הנבל, המורד, המורה, הרמאי, הקוסם, האם, הילד, המשרת וכדומה.
הארכיטיפים מופיעים לאורך כל ההיסטוריה במגוון של צורות, כולל דמויות מיתולוגיות, דמויות באמנות ובדתות השונות. ניתן למצוא אותם בסיפורים, סמלים, טקסים ומיתוסים שונים.
הראשון שבכתביו מופיעים ארכיטיפים הוא אפלטון, שכתב על התבניות הנצחיות שנמצאות בכל מקום ושיש להן היבטים שונים. הוא מזכיר למשל את תבנית היופי כתבנית נצחית, שהיא אמנם מופשטת אך ניתן למצוא אותה בעולם הרגיל, בצורות של אנשים, פרחים ויצירות יפות.
הפסיכולוג הנודע קרל גוסטב יונג חקר בתחילת המאה ה-20 את הדתות וחידש בתיאוריית הארכיטיפים שלו. הוא ראה בארכיטיפ תבנית מנטלית עולמית שבאה לידי ביטוי בכל התחומים.
רובנו נוהגים לספר סיפורים. חדשות, רכילות, אגדות, סרטים, סדרות וספרים הם רק חלק מעולם זה. אם מביטים היטב, ניתן לראות שמאחורי כל התנהגות מסתתר ארכיטיפ כלשהו, גיבור או נבל ובטוח שיש שם סיפור שממתין שיספרו אותו.
הנה דוגמאות של ארכיטיפים בתרבות המודרנית:
https://youtu.be/cZ0i5sayf20
על ארכיטיפים בתרבות, החל מהגיבור, הנבל, הרמאי והאנדרדוג:
http://youtu.be/TnSHTEn-gLA
ארכיטיפ הקוסם:
https://youtu.be/4unDD4OUUNQ
והסבר של הארכיטיפים, עם דוגמאות:
https://youtu.be/-9qVhIclcbI
ארכיטיפים (Archetypes) הם תבניות סימליות משותפות לעולם כולו. הארכיטיפים נמצאים בכל העולם ובכל התרבויות האנושיות כולן. הארכיטיפים הם תבניות של תפקידים שונים בחיים.
בין הארכיטיפים הידועים ניתן למצוא את הגיבור, האנדרדוג, הלוחם, הנבל, המורד, המורה, הרמאי, הקוסם, האם, הילד, המשרת וכדומה.
הארכיטיפים מופיעים לאורך כל ההיסטוריה במגוון של צורות, כולל דמויות מיתולוגיות, דמויות באמנות ובדתות השונות. ניתן למצוא אותם בסיפורים, סמלים, טקסים ומיתוסים שונים.
הראשון שבכתביו מופיעים ארכיטיפים הוא אפלטון, שכתב על התבניות הנצחיות שנמצאות בכל מקום ושיש להן היבטים שונים. הוא מזכיר למשל את תבנית היופי כתבנית נצחית, שהיא אמנם מופשטת אך ניתן למצוא אותה בעולם הרגיל, בצורות של אנשים, פרחים ויצירות יפות.
הפסיכולוג הנודע קרל גוסטב יונג חקר בתחילת המאה ה-20 את הדתות וחידש בתיאוריית הארכיטיפים שלו. הוא ראה בארכיטיפ תבנית מנטלית עולמית שבאה לידי ביטוי בכל התחומים.
רובנו נוהגים לספר סיפורים. חדשות, רכילות, אגדות, סרטים, סדרות וספרים הם רק חלק מעולם זה. אם מביטים היטב, ניתן לראות שמאחורי כל התנהגות מסתתר ארכיטיפ כלשהו, גיבור או נבל ובטוח שיש שם סיפור שממתין שיספרו אותו.
הנה דוגמאות של ארכיטיפים בתרבות המודרנית:
https://youtu.be/cZ0i5sayf20
על ארכיטיפים בתרבות, החל מהגיבור, הנבל, הרמאי והאנדרדוג:
http://youtu.be/TnSHTEn-gLA
ארכיטיפ הקוסם:
https://youtu.be/4unDD4OUUNQ
והסבר של הארכיטיפים, עם דוגמאות:
https://youtu.be/-9qVhIclcbI
מהי סדרת פיבונאצ'י?
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
סדרת פיבונאצ'י במתמטיקה היא סדרת מספרים שהאיברים הראשונים בה הם 1 ו-1. כל איבר אחר בסדרת פיבונאצ'י שווה לסכום של שני האיברים הקודמים לו. 2 שווה ל-1 ועוד 1, 3 שווה 2+1, 5 הוא 2+3 וכן הלאה.
הסדרה קרויה על שם המתמטיקאי לאונרדו דה פיזה (לאונרדו מהעיר פיזה) שבאיטליה, שכונה "פיבונאצ'י". פיבונאצ'י תיאר את הסדרה הזו ב"ספר החשבוניה" שיצא בשנת 1202. הוא השתמש בסדרת פיבונאצ'י כדי לתאר את מספר הצאצאים של זוג ארנבים אחד. הוא תאר מצב שכל זוג ארנבים מגיל חודשיים ומעלה, ממליט מדי חודש זוג נוסף, התוצאות של מספר הצאצאים שלהם יהיו על פי הסדרה הזו.
מסתבר שהיחס בין שני איברים עוקבים של מספרי פיבונאצ'י שואף ל"יחס הזהב", קבוע מתמטי שתואר כבר ביוון העתיקה. תמיד כשמחלקים שני איברים עוקבים בסדרת פיבונאצ'י, התוצאה תלך ותתקרב לחתך הזהב. בדרך זו מוסברים דברים רבים בטבע בעזרת סדרת פיבונאצ'י והרקורסיה (ראו באאוריקה בתגית "מה זה, רקורסיה"), מקונכיות עם "ספירלת הזהב", דרך פרחים, כרובית, גלקסיות חלזוניות ועוד. וזה לא במקרה שסדרת פיבונאצ'י היא כה נפוצה בטבע - כמו שהראינו קודם בדוגמת הארנבים, מדובר בצורה היעילה ביותר לשכפול וכשצמחים ובעלי חיים פשוטים משכפלים תאים בגדילה - מקבלים בדיוק את הסדרה של פיבונאצ'י.
מקובל לסמן את איברי הסדרה באות F, שמוגדרת ברקורסיה - כלומר פעולה המבוצעת על ידי הפניה עצמית. במקרה הזה, כל F הוא סכום שני ה-Fים שלפניו.
הנה הסבר על סדרת פיבונאצ'י (עברית):
https://youtu.be/EAXKR-H_bS0
הסבר מדעי של הסדרה הפיבונאצ'ית (עברית):
http://youtu.be/z5RWfXTd3QU
הדגמה של סדרת פיבונאצ'י:
http://youtu.be/H2aHh5FLX5w
והסבר מתמטי של סדרת ה פיבונאצ'י (מתורגם):
https://youtu.be/SjSHVDfXHQ4
איך ליצור רצועת מביוס לבד?
מהו הניסוי המתמטי במשטח נייר עם צד אחד בלבד?
האם אפשר ליצור משטח נייר עם צד אחד בלבד?
הנה ניסוי מדהים שמראה איך המתמטיקה היא דבר שאפשר להרגיש בידיים וכמה שהיא מופלאה. כל מה שצריך הוא פיסת נייר ארוכה ונייר דבק.
הנה סרטון עם ניסוי ליצירת רצועת מביוס בעצמך (עברית):
http://youtu.be/EaG4_EgIZPE
האם אפשר ליצור משטח נייר עם צד אחד בלבד?
הנה ניסוי מדהים שמראה איך המתמטיקה היא דבר שאפשר להרגיש בידיים וכמה שהיא מופלאה. כל מה שצריך הוא פיסת נייר ארוכה ונייר דבק.
הנה סרטון עם ניסוי ליצירת רצועת מביוס בעצמך (עברית):
http://youtu.be/EaG4_EgIZPE
מהם פרקטלים?
הפרקטל הוא צורה שככל שנביט בה קרוב יותר, נראה את אותה הצורה חוזרת על עצמה בכל קנה מידה. זוהי צורה גאומטרית שמורכבת פנימה, שוב ושוב, מעותקים של עצמה, מוקטנים יותר ויותר. ככל שנתבונן לתוך חלקי הפרקטל, נראה שם תמיד חלקים הדומים לו, כך שכל פרט זעיר בצורה, דומה לצורה המקורית והגדולה ביותר.
בגרפיקה ממוחשבת עושים המון שימוש בפרקטלים. הסיבה היא שנוסחאות מתמטיות קלות יחסית מאפשרות ליצור הרים ומרקמים מורכבים ליצירה בצורה אחרת. גם בפיזיקה משתמשים בפרקטלים למחקרים על תורת הכאוס וכדומה.
בטבע אפשר לראות מבנים שונים שדומים לפרקטלים. מבנים בטבע כמו צורת הכרובית, מבנה העורקים של העלה, התפצלות כלי הדם בגוף, פתית שלג או צורת קו חוף (במיוחד של הפיורדים בנורווגיה) - כל אלה מזכירים מאד את הפרקטלים ומראים שבטבע יש שיטה גם בדברים שאינם מובנים בצורה מתמטית.
הנה סרטון הסבר למושג הפרקטל (מתורגם):
http://youtu.be/Tm0U2VxFd8Q
הסבר מילולי על הפרקטלים - מהתבניות היותר מעניינות שבטבע (עברית):
http://youtu.be/ofA2tBvcbhw?t=3m38s
המתמטיקה של הפרקטלים בסרטון מקסים לפי ז'אנר הסרט האפל (מתורגם):
https://youtu.be/0C75vRVL5lE
הפרקטלים שבטבע:
https://youtu.be/XwWyTts06tU
עוד פרקטלים בטבע:
https://youtu.be/dZM45mfJQ40
להדגמת הרקורסיה הפשוטה, הנה משולש סרפינסקי שלא נגמר:
http://youtu.be/QsMvoui5WlQ?t=10s
ופרקטל מתמטי ללא סוף, בגרפיקה ממוחשבת ואנימציה מוסיקה נהדרים:
https://youtu.be/hRrBnI5L0u8?long=yes
הפרקטל הוא צורה שככל שנביט בה קרוב יותר, נראה את אותה הצורה חוזרת על עצמה בכל קנה מידה. זוהי צורה גאומטרית שמורכבת פנימה, שוב ושוב, מעותקים של עצמה, מוקטנים יותר ויותר. ככל שנתבונן לתוך חלקי הפרקטל, נראה שם תמיד חלקים הדומים לו, כך שכל פרט זעיר בצורה, דומה לצורה המקורית והגדולה ביותר.
בגרפיקה ממוחשבת עושים המון שימוש בפרקטלים. הסיבה היא שנוסחאות מתמטיות קלות יחסית מאפשרות ליצור הרים ומרקמים מורכבים ליצירה בצורה אחרת. גם בפיזיקה משתמשים בפרקטלים למחקרים על תורת הכאוס וכדומה.
בטבע אפשר לראות מבנים שונים שדומים לפרקטלים. מבנים בטבע כמו צורת הכרובית, מבנה העורקים של העלה, התפצלות כלי הדם בגוף, פתית שלג או צורת קו חוף (במיוחד של הפיורדים בנורווגיה) - כל אלה מזכירים מאד את הפרקטלים ומראים שבטבע יש שיטה גם בדברים שאינם מובנים בצורה מתמטית.
הנה סרטון הסבר למושג הפרקטל (מתורגם):
http://youtu.be/Tm0U2VxFd8Q
הסבר מילולי על הפרקטלים - מהתבניות היותר מעניינות שבטבע (עברית):
http://youtu.be/ofA2tBvcbhw?t=3m38s
המתמטיקה של הפרקטלים בסרטון מקסים לפי ז'אנר הסרט האפל (מתורגם):
https://youtu.be/0C75vRVL5lE
הפרקטלים שבטבע:
https://youtu.be/XwWyTts06tU
עוד פרקטלים בטבע:
https://youtu.be/dZM45mfJQ40
להדגמת הרקורסיה הפשוטה, הנה משולש סרפינסקי שלא נגמר:
http://youtu.be/QsMvoui5WlQ?t=10s
ופרקטל מתמטי ללא סוף, בגרפיקה ממוחשבת ואנימציה מוסיקה נהדרים:
https://youtu.be/hRrBnI5L0u8?long=yes
מהו יחס הזהב או חיתוך הזהב?
מדהים שחשבון יכול להיות קשור ליופי, לא?
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes
מדהים שחשבון יכול להיות קשור ליופי, לא?
אינכם מאמינים? - את יחס הזהב גילה ככל הנראה אחד מתלמידיו של הפילוסוף היווני פִּיתָגוֹרַס לפני כ-2,500 שנה. הוא שם לב שבני האדם הכי אוהבים צורה של מלבן שהיחס בין צלעותיו הוא יחס חשבוני של 1 ל-1.618. היחס הזה שיוצר "מלבן הזהב", יחס שמתקבל מחלוקת האורך שלו ברוחבו, התגלה כיפה בעיני אנשים בכל העולם. זהו "יחס הזהב" או "חיתוך הזהב", שמופיע במקומות רבים ובלתי-צפויים.
מאז הסתבר במחקרים שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, רובם ככולם היו בוחרים במלבן הזהב. זה מראה שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
ואכן, יחס הזהב, שיש שהמכנים גם "חתך הזהב", הוא יחס מתמטי שהמדע והאמנות עוסקים בו כבר מאות בשנים. תלמידי המתמטיקה מכירים אותו בתור המספר האי רציונלי שמסומן באות היוונית 'פִי' (φ). זהו מספר שמתחיל ב-1.6180339887 אבל הוא מכיל מספר אינסופי של ספרות אחרי הנקודה העשרונית.
יחס הזהב, שתואר לראשונה לפני כ-2,300 שנים בספר "יסודות" של אוקלידס, כונה אז "יחס קיצוני וממוצע". בתקופת הרנסאנס נכתבו מחקרים וספרים על "יחס הזהב" והוא קיבל את הכינוי "הפרופורציה האלוהית". בנו לפיו מבנים מפוארים, יצרו יצירות אמנות נשגבות, הלחינו מוסיקה ובמיוחד ראו אותו בטבע, כמעט בכל מקום.
התבוננות במלבן הזהב ממלאת בני האדם בתחושה של יופי ופרופורציה. כשמחלקים את אורכו של מלבן הזהב ברוחבו מקבלים את "יחס הזהב". היוונים הקדמונים והמצרים הקדמונים התייחסו אליו כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק, כולל הפירמידות במצרים והפרתנון שבאקרופוליס של אתונה. באומנות מופיע יחס הזהב ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
כאמור, בנוסף לאמנות, אדריכלות ותחומי אסתטיקה אחרים שמשתמשים לא מעט ביחס הזהב, גם בטבע ניתן לראותו, במבנים של קונכיות ושבלולים, בסידור העלים מסביב לגבעולים, במערבולות, סופות טורנדו ועד לגלקסיות חלזוניות.
יש גם טענה שיחס הזהב הוא שמסביר את העובדה שאנו שכולנו מזהים את אותן פנים יפות ומבנה גוף יפה. כאן כמובן שיש מחלוקות, כי הוכח לא פעם שגם אם פנים שבנויות על פי יחס הזהב הן יפות, הרבה פנים שנחשבים יפים בקרב הציבור, כמו מרילין מונרו למשל, לא מחולקים על פי יחס הזהב.. האם הם מכוערים?
הנה סרטון הסבר על יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
יחס הזהב והקשר בינו לבין מה שאנו רואים כיופי (מתורגם):
http://youtu.be/_cIlomNxxig
יחס הזהב דרך סדרת פיבונאצ'י, בה יש בין כל שני מספרים יחס הנוטה ליחס הזהב (מתורגם):
http://youtu.be/z5RWfXTd3QU
איך יחס הזהב בונה את המלבנים שהקשתות שעוברות בהם יוצרות את סדרת פיבונאצ'י:
http://youtu.be/kkGeOWYOFoA
ההקשרים השונים של פי ויחס הזהב:
http://youtu.be/0hvD5kLqjuw
וסרט תיעודי על יחס הזהב:
https://youtu.be/gLml9nltl6M?long=yes
איפה יש פרקטלים בטבע?
ודאי היכרתם או קראתם באאוריקה על הפרקטלים, אותן צורות מתמטיות מיוחדות שהתגלו על ידי חוקר הפרקטלים בנואה מנדלברוט והעסיקו חוקרים רבים מתחילת המאה ה-20.
את הפרקטלים ניתן לזהות בכך שיש להם דמיון עצמי. כלומר, כל חלק בהם דומה לדבר השלם. גם בטבע ישנם לא מעט דברים שאם נביט בחלק קטן מהם נגלה את אותה צורה של השלם - בקנה מידה קטן. וגם בחלק הקטן הזה, אם נביט בעזרת זכוכית מגדלת, נוכל לראות שחלקיו שלו דומים גם הם לשלם וחלק הזה וכך זה יכול להמשיך עוד ועוד פנימה. תמיד אותה צורה ושמה...
אז אומרים לכם שכל כך הרבה פרקטלים יש בטבע ואפשר לראותם כמעט בכל מקום. אבל איפה זה בדיוק בכל מקום?
ובכן, בכרובית, בברקים, בריאות, שרכים, מפלים, בפתיתי שלג, בנימי העלה, בענפי העצים, גבישי הקרח, בענני קומולוס, בכלי הדם שלנו, בבועות סבון, בחופי ים מפורצים של פיורדים נורווגיים או בחופי אגמים כמו אגם נאצר שבמצרים, בשוניות אלמוגים במעמקי הים ועד לגלקסיות הענקיות שבחלל.
כן. בטבע נוכל למצוא צורות רבות שיש להן תכונות פרקטליות. דוגמה מפורטת היא לצלם את אורכו של חוף ים ממטוס ולראות שצורתו דומה מאד לזו שנראה בטיול לאורך החוף, כשנביט בפרטים הקטנים שלו. גם מדידת אורכו של קו החוף תגלה לנו דבר מדהים - אורכו הוא בפשטות אינסופי. זה קורה משום שקנה המידה משפיע על המדידה. אם נחשב אורך חוף מתמונת לוויין נקבל אורך קטן בהרבה מזה שיתקבל אם נמדוד את הדרך שעושה נמלה ההולכת לאורכו. הסיבה היא שהשיפולים והשיפועים שחווה הנמלה בקו החוף מאריכים לה את הדרך בטירוף. זה סוג של פרקטל - הנמלה רואה את צורת קו החוף, שהיא זהה לצורה שמצלם הלווים מהחלל.
פרקטלית היא גם הכרובית למשל. אם נחתוך אותה לאורך, נראה שיש בה התפצלויות שיוצרות המון כרוביות קטנות, שבעצמן מתפצלות כל אחת לכרוביות זעירות, שבכל אחת יש כרוביות מיקרוסקופיות והלאה.
בצורה דומה מתפצלות הריאות שלנו או כלי הדם שבגופנו. אבל אתם לא יכולים להביט אל תוך הלב, אז קחו עלה של עץ או שיח ושימו לב לנימים של העלה. נכון שהם מסתעפים ומתפצלים עוד ועוד, כשמכל נים יוצאים נימים קטנים, שמהם יוצאים נימים זעירים וכך הלאה? - גם בכלי הדם שבגופנו יוצאים כך עשרות כלי דם קטנים מכל אחד, בתבנית החוזרת על עצמה שוב ושוב, עד לנימים זעירים ודקיקים במיוחד.
הנה הפרקטלים שבטבע ותגליתו של מנדלברוט:
https://youtu.be/w_MNQBWQ5DI
הסבר הפרקטלים שבטבע:
https://youtu.be/Tm0U2VxFd8Q
שלל פרקטלים טבעיים:
https://youtu.be/4IRLvYOZD8A
עוד פרקטלים בטבע:
https://youtu.be/XwWyTts06tU
ואובייקטים טבעיים שהם פרקטלים:
https://youtu.be/dZM45mfJQ40
ודאי היכרתם או קראתם באאוריקה על הפרקטלים, אותן צורות מתמטיות מיוחדות שהתגלו על ידי חוקר הפרקטלים בנואה מנדלברוט והעסיקו חוקרים רבים מתחילת המאה ה-20.
את הפרקטלים ניתן לזהות בכך שיש להם דמיון עצמי. כלומר, כל חלק בהם דומה לדבר השלם. גם בטבע ישנם לא מעט דברים שאם נביט בחלק קטן מהם נגלה את אותה צורה של השלם - בקנה מידה קטן. וגם בחלק הקטן הזה, אם נביט בעזרת זכוכית מגדלת, נוכל לראות שחלקיו שלו דומים גם הם לשלם וחלק הזה וכך זה יכול להמשיך עוד ועוד פנימה. תמיד אותה צורה ושמה...
אז אומרים לכם שכל כך הרבה פרקטלים יש בטבע ואפשר לראותם כמעט בכל מקום. אבל איפה זה בדיוק בכל מקום?
ובכן, בכרובית, בברקים, בריאות, שרכים, מפלים, בפתיתי שלג, בנימי העלה, בענפי העצים, גבישי הקרח, בענני קומולוס, בכלי הדם שלנו, בבועות סבון, בחופי ים מפורצים של פיורדים נורווגיים או בחופי אגמים כמו אגם נאצר שבמצרים, בשוניות אלמוגים במעמקי הים ועד לגלקסיות הענקיות שבחלל.
כן. בטבע נוכל למצוא צורות רבות שיש להן תכונות פרקטליות. דוגמה מפורטת היא לצלם את אורכו של חוף ים ממטוס ולראות שצורתו דומה מאד לזו שנראה בטיול לאורך החוף, כשנביט בפרטים הקטנים שלו. גם מדידת אורכו של קו החוף תגלה לנו דבר מדהים - אורכו הוא בפשטות אינסופי. זה קורה משום שקנה המידה משפיע על המדידה. אם נחשב אורך חוף מתמונת לוויין נקבל אורך קטן בהרבה מזה שיתקבל אם נמדוד את הדרך שעושה נמלה ההולכת לאורכו. הסיבה היא שהשיפולים והשיפועים שחווה הנמלה בקו החוף מאריכים לה את הדרך בטירוף. זה סוג של פרקטל - הנמלה רואה את צורת קו החוף, שהיא זהה לצורה שמצלם הלווים מהחלל.
פרקטלית היא גם הכרובית למשל. אם נחתוך אותה לאורך, נראה שיש בה התפצלויות שיוצרות המון כרוביות קטנות, שבעצמן מתפצלות כל אחת לכרוביות זעירות, שבכל אחת יש כרוביות מיקרוסקופיות והלאה.
בצורה דומה מתפצלות הריאות שלנו או כלי הדם שבגופנו. אבל אתם לא יכולים להביט אל תוך הלב, אז קחו עלה של עץ או שיח ושימו לב לנימים של העלה. נכון שהם מסתעפים ומתפצלים עוד ועוד, כשמכל נים יוצאים נימים קטנים, שמהם יוצאים נימים זעירים וכך הלאה? - גם בכלי הדם שבגופנו יוצאים כך עשרות כלי דם קטנים מכל אחד, בתבנית החוזרת על עצמה שוב ושוב, עד לנימים זעירים ודקיקים במיוחד.
הנה הפרקטלים שבטבע ותגליתו של מנדלברוט:
https://youtu.be/w_MNQBWQ5DI
הסבר הפרקטלים שבטבע:
https://youtu.be/Tm0U2VxFd8Q
שלל פרקטלים טבעיים:
https://youtu.be/4IRLvYOZD8A
עוד פרקטלים בטבע:
https://youtu.be/XwWyTts06tU
ואובייקטים טבעיים שהם פרקטלים:
https://youtu.be/dZM45mfJQ40
מהי הפרופורציה האלוהית?
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
זה קרה בשנת 1202 כשמתמטיקאי קדום ורב זכויות סיפר את סיפור הארנבים, שמולידים צאצא אחד בכל חודש ומתרבים בקצב לוגריתמי. הוא הציג לעולם סדרת מספרים שסכום כל שני מספרים עוקבים בה יהיה המספר הבא. אבל הסדרה הזו צפנה סודות נוספים ומדהימים. תוכלו ללמוד עליהם לעומק באאוריקה, בתגית "סדרת פיבונאצ'י".
אבל המעניין הוא שכמעט מבלי משים חשף פיבונאצ'י בתגלית שלו את אחד מסודות האסתטיקה המעניינים בהיסטוריה. הוא גילה שיופי ומתמטיקה הלכו במשך אלפי שנים יד ביד, כשאמנים, אדריכלים ויוצרים מכל הזמנים אחזו בתפיסת יופי ואסתטיקה דומים, מבלי לתאם זאת ביניהם.
ועוד יותר, הוא זיהה שהתפיסה הזו טבעית ומשותפת לכל בני האדם, בלי הבדל של תרבות, מקום וזמן. בכל כיוון שאליו נפנה מבט, נוכל לראות את אצבע אלוהים, או לפחות את מודל היופי שהוא יצר בטבע ושבאופן בלתי תלוי אימצו כל התרבויות העתיקות. מקונכיות וחלזונות, דרך פרחים ואיצטרובלים ועד לגלקסיות שלמות - הטבע מוצף ביחס הזהב שגילה פיבונאצ'י.
מסתבר שהמתמטיקה גילתה את הדרך היעילה ביותר לשכפול של תאים ולתנועה בחלל וזו, אם תרצו, יצרה פרופורציה שכולה אצבע אלוהים.
הנה הפרופורציה האלוהית שהלכה והתגלתה מאז פיבונאצ'י:
http://youtu.be/03uC9bhX0Rc
הדוגמאות הרבות של הפרופורציה האלוהית בעולם:
http://youtu.be/0hvD5kLqjuw
קבלו נסיון לבחון את המונה ליזה וכיצד יצר לאונרדו, כמו אמנים רבים, תמונה עם פרופורציות מושלמות שלמד מהטבע:
http://youtu.be/JFTSAjZEqPw
הסבר של הפרופורציה האלוהית וטענה די מוזרה שמסתירים אותה מהציבור:
http://youtu.be/4VrcO6JaMrM
וסרטון תיעודי על המתמטיקה המופלאה של פיבונאצ'י שמייצרת את היופי הזה:
https://youtu.be/keLN89CWZ-A?long=yes
מהו מלבן הזהב?
מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes
מסתבר שאם היו אנשים רבים ומגוונים מכל העולם והתקופות נשאלים איזה מרובע מבין מספר מרובעים שלפניהם הוא היפה והנעים ביותר לעין, היו בוחרים רובם ככולם במלבן הזהב. מלבן הזהב הוא מלבן שהיחס בין אורכו לרוחבו הוא יחס שזכה גם הוא לכינוי יחס הזהב. כשהאורך של מלבן גדול פי בערך 1.618 מהרוחב שלו, מתקיים יחס מושלם ביניהם והוא נקרא מלבן הזהב. מלבן הזהב מוכיח שהיופי הוא אובייקטיבי, כלומר לא תלוי בתקופה, תרבות או אמונה.
כיוון שיחס הזהב הוא כה יפה ומושלם בעיני המתבוננים, הוא זכה לכינוי 'הפרופורציה האלוהית'. אלא שיחס הזהב נמצא כנכון ומתאים לא רק באומנות שעשה האדם, אלא קודם כל בטבע עצמו. כי מעולם הטבע הגיע יחס הזהב והמספר פי לעולם האומנות. ומאז ומתמיד הוא מופיע באדריכלות, במבנים המושלמים והיפים בהיסטוריה, ובאומנות - ברבים מהציורים שבהם יש יחס פרופורציוני בין גדלים שונים.
עמים קדומים כמו היוונים הקדמונים והמצרים הקדמונים התייחסו למלבן הזהב כשיא היופי האסתטי ותכננו לפיו מבנים מהיפים ביותר בעולם העתיק. בין המבנים שבנויים בהקפדה של יחס הזהב או מלבן הזהב, ניתן למצוא את הפירמידות במצרים, הפרתנון שבאקרופוליס של אתונה הטאג' מהאל שבהודו.
הנה מלבן הזהב שיוצר את הספירלות המיוחדות כל כך על פי יחס הזהב:
http://youtu.be/kkGeOWYOFoA
המתמטיקה של יחס הזהב (עברית):
https://youtu.be/co2k2bcZ1h0
ההופעות הרבות של יחס הזהב ומלבן הזהב:
http://youtu.be/0hvD5kLqjuw
והמקומות המפתיעים מסביב שבהם ניתן לפגוש אותו:
https://youtu.be/RqqErDSLtwE?long=yes
